In defense of a non-newtonian economic analysis through an accounting paradigm
This paper is closed for comments.
Abstract
The double-entry bookkeeping promoted by Luca Pacioli in the fifteenth century could be considered a strong argument in behalf of the multiplicative calculus which can be developed from the Grossman and Katz non-newtonian calculus concept provided that one goes from an additive bookkeeping system to a multiplicative one. In order to emphasize this statement, we present a brief history of the accountancy in its early time and we make the point of Ellermans research concerning the double-entry bookkeeping. The most astonishing point linked to this subject is to realize that not only the
calculus, but also the accounting systems, have been the subjects of path dependency.
For some time now, Professors Filip and Piatecki (F&P) have promoted the use of the non-Newtonian calculus developed in a little-known book: Grossman, Michael, and Robert Katz. 1972. Non-Newtonian Calculus. Pigeon Cove MA: Lee Press. F&P treat the non-Newtonian calculus as if it were a major (but neglected) discovery that will shed light on many issues, e.g., growth theory. In this calculus, the additive operations involved in defining the usual (“Newtonian”) derivative are replaced by multiplicative operations, and then a whole set of analogous results are derived.
Firstly, it should be noted that this is not the discovery of new mathematics but a novel way to derive and present well-known results about exponentials as Grossman & Katz themselves indicate in the section of their book entitled “Relationships to the Classical Calculus” [pp. 16-17]. The way in which logarithms and exponentials interchange additive and multiplicative operations, e.g.,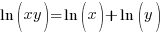
and 
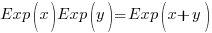, is all part of ordinary post-Euler calculus, and need not be seen as a “non-Newtonian calculus” juxtaposed to “Newtonian calculus.”
Secondly, it may be useful to restate certain formulas in a different way as when the Cobb-Douglas production function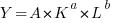
is linearized as 
in order to apply linear regression. It may well be that certain formulas in growth theory may be better understood by using logarithms and exponentials to switch between additive and multiplicative versions, but that can all be done using standard calculus. There is no need whatsoever to use Grossman & Katz’s idiosyncratic notation and terminology as if it were some new exotic mathematics. F&P’s cited paper in a Bulgarian mathematics journal on applying the non-newtonian calculus to growth theory might well be translated into ordinary terms to see if it is really saying something new and significant.
In any case, the paper under review here is an attempt to somehow argue that my recent work on the mathematical formulation of double-entry bookkeeping lends support to using non-newtonian analysis. In an apparent effort to explain the “locked-in” use of additive arithmetic in ordinary accounting, F&P spend much of the paper in giving a history of accounting.
Then F&P spend the remainder of the paper attempting to give a synopsis of the mathematical treatment of double-entry bookkeeping in an additive and multiplicative form. But they completely bungle the mathematics of the usual additive case, and then their attempt to give a multiplicative version is complete gibberish. If my past writings on the topic have been too mathematically challenging, then I would recommend a recent paper in an accounting education journal that attempts to explain the mathematical treatment at least to accounting professors, if not to mathematically-inclined accountants: Ellerman, David. 2014. “On Double-Entry Bookkeeping: The Mathematical Treatment.” Accounting Education: An International Journal 23 (5 (Oct.)): 483–501 [which can be downloaded from my website: http://www.ellerman.org].
And even if F&P straighten out the math, it still has no connection to their attempt (which is ill-conceived in the first place) to gain insights by restating standard parts of the calculus (logs and exponentials) using the Grossman & Katz notation and terminology.
Leaving aside this particular paper, I would like to say a few words in favor of F&P’s use of additive and multiplicative analogies as a possible engine of discovery. I have much used additive-multiplicative analogies in my own work. In my 1995 book of essays, Intellectual Trespassing as a Way of Like [downloadable from my website], I explicitly mentioned the “additive-multiplicative engine of discovery.”
“Four of the essays in this book exploit one particular analogy that is mathematically captured in group theory. The real numbers with the operation of addition is an example of a group. The positive reals (excluding zero) with the operation of multiplication is another example of a group (indeed, the mapping of
from the reals to the positive reals shows that the two groups have the same mathematical structure). In some domains of science an additive group will have a key role, while in others a multiplicative group will capture the important relationships.”
“One simple engine of discovery is to systematically transfer some structure developed for the additive case over into the multiplicative case in another field, or to go the other way. This type of transfer between fields is illustrated in the essays on double-entry bookkeeping, arbitrage, valuation rings, and series-parallel duality.” [p. 2]
For instance, in electrical circuit theory, Kirchhoff’s voltage law says that around any closed loop in a circuit, the sum of the voltages between the nodes in the loop must sum to 0. The multiplicative version characterizes an arbitrage-free circle of exchanges (without transactions costs), i.e., that the rates of exchange around circle must multiply to 1.
Hence I would be the last to criticize F&P’s general methodology of using additive-multiplicative relationships as an engine of discovery. Indeed, I have long had a copy of Grossman & Katz’s book in my library—although I eventually concluded that their innovations were mainly at the presentational and terminological level.
Other engines of discovery that might be mentioned are symmetry arguments and duality theories. For instance, one of the simplest forms of symmetry is between the positive and negative numbers in the additive group of integers or real numbers. Keeping this symmetry in mind can be quite important in economics. In heterodox economics, the alternative to the disastrous labor theory of value is the labor theory of property which is often sloganized as “Labor’s right to the whole product” [Menger, Anton. 1899. The Right to the Whole Produce of Labour: The Origin and Development of the Theory of Labour’s Claim to the Whole Product of Industry. London: Macmillan and Co]. Yet the phrase “whole product” is often interpreted as just referring to the positive product of the outputs—as if there were no inputs that had to be used-up in the production of those outputs. Anyone accustomed to thinking in more symmetrical terms would immediately see that the phrase “whole product” has to include the negative terms representing the liabilities for the used-up inputs. Yet it is amazing how many economists, orthodox or heterodox, have trouble understanding that there is also a negative part of the “whole product”, i.e., that both assets and liabilities are created in production.
Thus I would certainly recommend the use of additive-multiplicative analogies, symmetry principles, and duality arguments as engines of discovery. But that does not mean that every result thus obtained is significant. In the words of Kenny Rogers’ song: “You’ve got to know when to hold ’em & Know when to fold ’em.”
The comments by David Ellerman, who incidentally was the first addressee of our work at least two years ago, are always welcomed. There is two part in his comment : in the first, he has formulated a strong critic against our work, and we need to answer and justify our approach. For the second part, we are on the same wavelength, so it needs no comments.
Regarding the comment “F&P treat the non-Newtonian calculus as if it were a major (but neglected) discovery that will shed light on many issues, e.g., growth theory”, one can find an emerging interest on the application of the non-newtonian calculus in the last years around the world — there is nearly a hundred papers, which use this technical in the last ten years.
If it rests on the fact that there is a passage between the multiplicative and the additive approach, we have explicitly acknowledge the point in the introduction when we say that \textit{there is a gangway to go from newtonian to non-newtonian derivative}. As it was not the object of the paper, we have decided not to go onto the maths. It is the reason why we have no appendix describing the non-newtonian derivative. Incidentally, if there was not such a gangway, it would be possible that we do not find the same optimum of a positive function by looking for it with the one or the other approach which would seems awkward.
But that’s not the point. When we have discovered the many facets of the work of Grossman and Katz, which goes far beyond the discovery of the multiplicative calculus, our first reaction was to let it in the shelves as no more than a mere curiosity which could not give any new insight about the economic analysis. For one of us, it took twenty years. Then we have decided to see if there was something to learn from it. Unfortunately, it was not clear how to use it, because of the two directions gangway. To explore some new model, we finally find that what must be done was to use accordingly some new definition of the balance equations. It was clear for us, it would be wise to define some multiplicative balance equations which could fit with the multiplicative derivative. Fortunately, both trick melt nicely in the case of exogenous economic growth to the restriction that we were also obliged to redefine capital obsolescence.
So with a beautiful naivety, we send the result in a mathematical economic journal whose name is without any importance. Big was our surprise to see our paper rejected, not because we used the Grossman/Katz non-newtonian derivative, but because the reviewer asserted that our balance equation — the standard macroeconomic balance, rewritten as a multiplicative balance — was not a balance equation. Not wanting to give in to discouragement, and always convinced that our approach could be of interest for some of our economist colleagues always in search of new specifications, we decided to write a paper explaining how additive accounting is a convention which should be replaced by an other one, since we found an other way to write a balance sheet.
So we decided to work on the history of accounting, to show how the incredible incunabula impetus of Paccioli destroyed any vague desire to organize the bookkeeping differently. Just in that time, we discovered the works of David Ellerman. In our conception, it was not possible to ignore them. It would have been plagiarism.
But, whichever be its quality, the salience of the additive accounting is such that, each time we were presenting our paper, invariably comes the question of the zero — in multiplicative accounting, its role is given to one. It is the reason why we have developed a very simple example to show how we can manage a multiplicative accounting.
And now we have had two papers, this one, non technical, submitted to Economic Thought and the other more technical and devoted to the exogenous economic growth. But the former was a justification of the multiplicative balance incorporated in the later. It was not possible to try to publish this one without having published the other. The opportunity arises to publish in a Bulgarian review which was perhaps a second best, as it is not an economic review, but this was necessary in order to be able to cite it —~incidentally, its open access policy was one of the reason for our decision. In publishing in Mathematica AEterna, we acquired a visibility which could not have been acquired in waiting for the acceptance of a more standard economic review. One must also note that during the four years or a little more we have been involved with this approach, which is new not in time but in use, a small but dynamic community of mathematicians have extended the Grossman-Katz work.
Obviously, our multiplicative bookkeeping example seems childish, but one must keep in mind that it was constructed only to show to macro-economists that the approach was workable. The Ellerman’s papers and books and their mathematical content was an inspiration source for us, but it was too extensive for our purpose.
Just a last point. Right now, inside the standard bookkeeping paradigm, we are working through the multiplicative derivative with a new inter-temporal criterion distinct from the Samuelson inter-temporal utility since one can define multiplicative integration in a similar way as the Cauchy-Riemann one. Of course, in all likelihood, it would perhaps not revolutionize the common approach to inter-temporal choices, but it gives some workable alternative in a field were, until now, there is not.
I have been invited to comment on the Filip and Piatecki paper relating non-newtonian economic analysis and double-entry bookkeeping (DEB). I have read the paper (many times…). I have read the 2 posted comments by Ellerman, plus reply. I have not read any other references suggested, though I shall eventually read the David Ellerman paper from Accounting Education. My thoughts are therefore relatively ‘clean’.
I approach this material from a diametrically opposite direction to the above three writers. I am an (emeritus) professor of accounting and not a mathematician at all. I am lnterested in the obscure and I am interested in history. This material satisfies both interests! I have an unpublished (co-authored) paper on Pacioli, linking together his love of mathematics, proportion (divina proportione), and the postulated parallelism between the desired absolution from spiritual sins through catholic confession, and the desired absolution from earthly sins through the proper application of DEB. Others can be obscure too…..I shall propose to my co-author that we submit the paper to this journal for open comment.
But taking the paper as on the website. First of all, the English is pretty terrible. Secondly, as Ellerman indicates, the balance of the paper is strange, with a long historical exposition of DEB, and then a sudden jump to two mathematical expositions of DEB. Neither really seems necessary for the other.
On the first part, the coverage seems extensive, but partial. There is actually much debate about what ‘DEB’ precisely is. It is certainly not synonymous with writing a figure down twice. The Merdiban (‘ladder’) method of bookkeeping used by the Ottoman empire state accounting system for some 600 years involved writing an amount twice (in an inset pattern resembling stairs or a ladder), but it was not DEB (despite recent articles claiming that it was!). Conversely a matrix presentation (debits vertical and credits horizontal, or vice versa), is DEB even though it writes the amount only once. DEB is, as Pacioli and Filip and Piatecki all understand, a cleverly constructed mathematical system with significant built-in checking devices, and significant power as the basis for analysis. But anyway the relevance of this long exposition to the essentially mathematical nature of the paper seems doubtful.
Turning to section 2.2, and the mathematical treatments of DEB, I note that Ellerman states that the authors ‘completely bungle the mathematics of the usual additive case’ and that the ‘multiplicative version is complete gibberish’. The additive method, to me, seems unnecessarily complicated, but this is as nothing compared with the multiplicative group. I appreciate that adding 0 in the first case has the same effect as multiplying by 1 in the second case. But this seems an excessively pragmatic reason for doing it…..Why bother???
I think my overall conclusions, based on a certain amount of intelligence and also on a large amount of ignorance, would be that
1) DEB is rather clever, and very interesting both technically and historically/socially. This paper does not develop this.
2) Mathematical arguments should be developed mathematically, for and by mathematicians.
3) On the reference in the abstract to path dependency (never mentioned in the paper itself!!), DEB is a tool to be used; if it ain’t broke, don’t fix it.
I realise that I contribute nothing to the mathematical objectives of the original paper. But I suspect that the paper itself, as designed and structured, doesn’t contribute much either.